Dask and Scikit-Learn -- Model Parallelism
Posted on July 11, 2016
Note: This post is old, and discusses an experimental library that no longer
exists. Please see this post on dask-searchcv,
and the corresponding
documentation for the current
state of things.
This is the first of a series of posts discussing some recent experiments combining dask and scikit-learn. A small (and extremely alpha) library has been built up from these experiments, and can be found here.
Before we start, I would like to make the following caveats:
- I am not a machine learning expert. Do not consider this a guide on how to do machine learning, the usage of scikit-learn below is probably naive.
- All of the code discussed here is in flux, and shouldn't be considered stable or robust. That said, if you know something about machine learning and want to help out, I'd be more than happy to receive issues or pull requests :).
There are several ways of parallelizing algorithms in machine learning. Some algorithms can be made to be data-parallel (either across features or across samples). In this post we'll look instead at model-parallelism (use same data across different models), and dive into a daskified implementation of GridSearchCV.
What is grid search?
Many machine learning algorithms have hyperparameters which can be tuned to improve the performance of the resulting estimator. A grid search is one way of optimizing these parameters — it works by doing a parameter sweep across a cartesian product of a subset of these parameters (the "grid"), and then choosing the best resulting estimator. Since this is fitting many independent estimators across the same set of data, it can be fairly easily parallelized.
Grid search with scikit-learn
In scikit-learn, a grid search is performed using the GridSearchCV class, and
can (optionally) be automatically parallelized using
joblib.
This is best illustrated with an example. First we'll make an example dataset for doing classification against:
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=10000,
n_features=500,
n_classes=2,
n_redundant=250,
random_state=42)
To solve this classification problem, we'll create a pipeline of a PCA and a
LogisticRegression:
from sklearn import linear_model, decomposition
from sklearn.pipeline import Pipeline
logistic = linear_model.LogisticRegression()
pca = decomposition.PCA()
pipe = Pipeline(steps=[('pca', pca),
('logistic', logistic)])
Both of these classes take several hyperparameters, we'll do a grid-search across only a few of them:
#Parameters of pipelines can be set using ‘__’ separated parameter names:
grid = dict(pca__n_components=[50, 100, 250],
logistic__C=[1e-4, 1.0, 1e4],
logistic__penalty=['l1', 'l2'])
Finally, we can create an instance of GridSearchCV, and perform the grid
search. The parameter n_jobs=-1 tells joblib to use as many processes as I
have cores (8).
from sklearn.grid_search import GridSearchCV
estimator = GridSearchCV(pipe, grid, n_jobs=-1)
%time estimator.fit(X, y)
What happened here was:
- An estimator was created for each parameter combination and test-train set (scikit-learn's grid search also does cross validation across 3-folds by default).
- Each estimator was fit on its corresponding set of training data
- Each estimator was then scored on its corresponding set of testing data
- The best set of parameters was chosen based on these scores
- A new estimator was then fit on all of the data, using the best parameters
The corresponding best score, parameters, and estimator can all be found as attributes on the resulting object:
estimator.best_score_
estimator.best_params_
estimator.best_estimator_
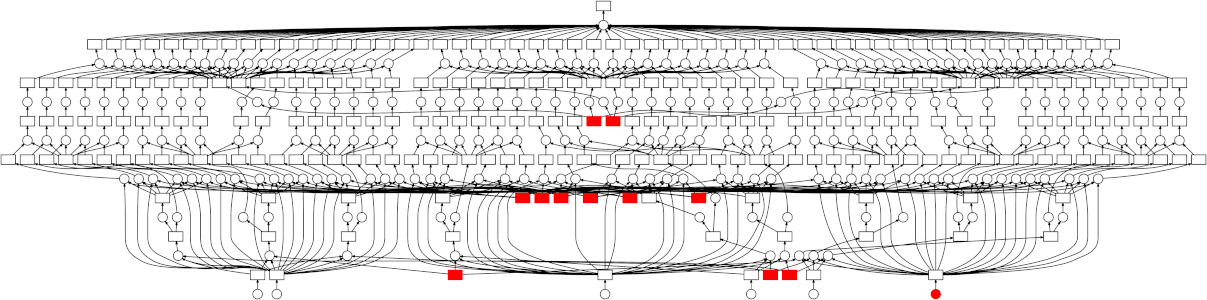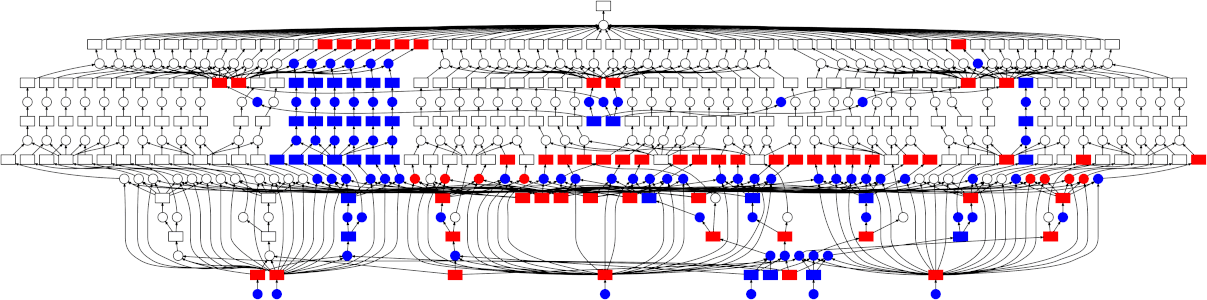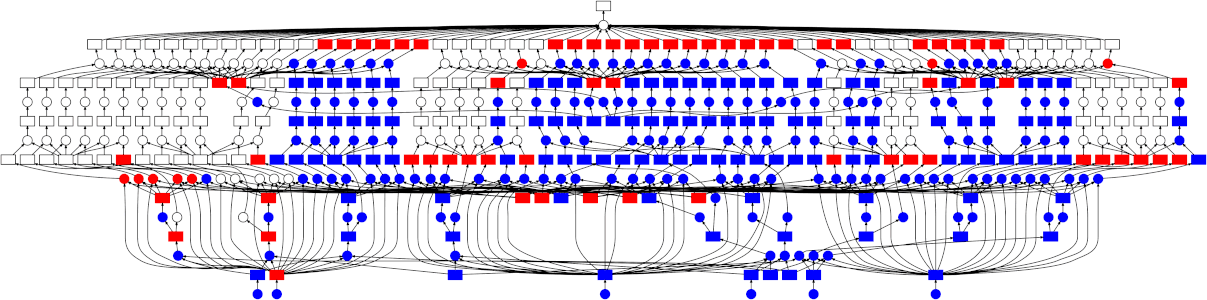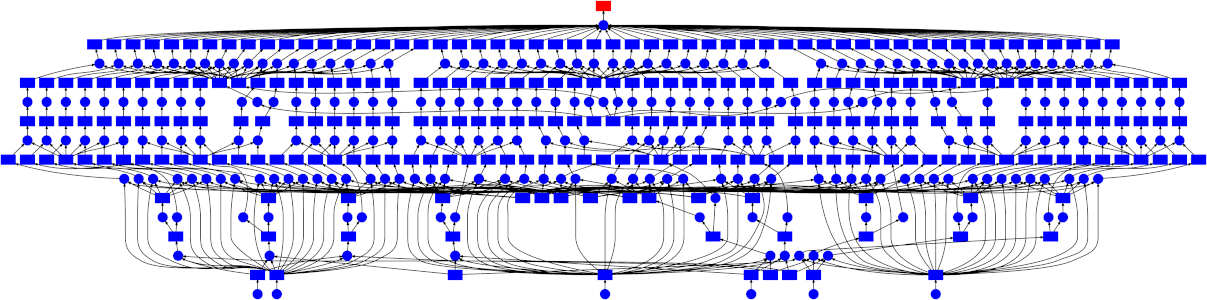 Looking at the trace, a few things stand out:
- We do a good job sharing intermediates. Each step in a pipeline is only fit
once given the same parameters/data, resulting in some intermediates having
many dependent tasks.
- The scheduler does a decent job of quickly finishing up tasks required to
release data. This doesn't matter as much here (none of the intermediates
take up much memory), but for other workloads this is very useful. See Matt
Rocklin's [excellent blogpost
here](http://matthewrocklin.com/blog/work/2015/01/06/Towards-OOC-Scheduling)
for more discussion on this.
## Distributed grid search using dask-learn
The [schedulers](http://dask.pydata.org/en/latest/scheduler-overview.html) used
in dask are configurable. The default (used above) is the threaded scheduler,
but we can just as easily swap it out for the distributed scheduler. Here I've
just spun up two local workers to demonstrate, but this works equally well
across multiple machines.
::Python
from distributed import Executor
# Create an Executor, and set it as the default scheduler
exc = Executor('10.0.0.3:8786', set_as_default=True)
exc
Looking at the trace, a few things stand out:
- We do a good job sharing intermediates. Each step in a pipeline is only fit
once given the same parameters/data, resulting in some intermediates having
many dependent tasks.
- The scheduler does a decent job of quickly finishing up tasks required to
release data. This doesn't matter as much here (none of the intermediates
take up much memory), but for other workloads this is very useful. See Matt
Rocklin's [excellent blogpost
here](http://matthewrocklin.com/blog/work/2015/01/06/Towards-OOC-Scheduling)
for more discussion on this.
## Distributed grid search using dask-learn
The [schedulers](http://dask.pydata.org/en/latest/scheduler-overview.html) used
in dask are configurable. The default (used above) is the threaded scheduler,
but we can just as easily swap it out for the distributed scheduler. Here I've
just spun up two local workers to demonstrate, but this works equally well
across multiple machines.
::Python
from distributed import Executor
# Create an Executor, and set it as the default scheduler
exc = Executor('10.0.0.3:8786', set_as_default=True)
exc